Der Hauptunterschied zwischen kontinuierlichem und diskretem Spektrum besteht darin, dass ein kontinuierliches Spektrum keine diskreten Linien aufweist, während ein diskretes Spektrum nur diskrete Linien enthält.
Die Begriffe kontinuierliches Spektrum und diskretes Spektrum sind das Gegenteil von einander. Aus den für eine bestimmte physikalische Größe gewonnenen Werten kann ein Spektrum erstellt werden. Das Vorhandensein oder Fehlen von Lücken zwischen diesen Werten kann ein diskretes bzw. kontinuierliches Spektrum erzeugen.
Was ist kontinuierliches Spektrum?
Ein kontinuierliches Spektrum ist eine Reihe von erreichbaren Werten einer physikalischen Größe, wobei zwischen den einzelnen Werten keine beträchtliche Lücke besteht. Diese Wertereihe ist das Gegenteil des diskreten Spektrums. Die zum Aufbau eines kontinuierlichen Spektrums verwendeten Werte können Energie, Wellenlänge usw. sein.
Das häufigste Beispiel für ein kontinuierliches Spektrum ist das Spektrum des Lichts, das von angeregten Wasserstoffatomen emittiert wird. Dieses Spektrum entsteht durch freie Elektronen, die an ein Wasserstoffion gebunden werden und Photonen emittieren, die dazu neigen, sich gleichmäßig über einen weiten Wellenlängenbereich auszubreiten.
Der Begriff kontinuierliches Spektrum wird meistens verwendet, wenn der Wertebereich für die physikalische Größe (hauptsächlich Energie oder Wellenlänge) sowohl kontinuierliche als auch diskrete Teile hat, entweder gleichzeitig oder zu verschiedenen Zeiten. Dies liegt daran, dass die Position und der Impuls eines freien Teilchens ein kontinuierliches Spektrum haben und wenn das Teilchen auf einen begrenzten Raum beschränkt ist, wird sein Spektrum zu einem diskreten Spektrum. Üblicherweise werden quantenchemische Systeme mit freien Teilchen assoziiert (z. B. Atome in einem Gas, Elektronen in einem Elektronenstrahl, Leitungsbandelektronen in einem Metall usw.).
Was ist ein diskretes Spektrum?
Ein diskretes Spektrum ist eine Reihe erreichbarer Werte einer physikalischen Größe mit einer positiven Lücke zwischen jedem Wert. Dies steht im Gegensatz zum kontinuierlichen Spektrum. Diese Art von Spektrum entsteht, wenn Elektronen aus einem gebundenen Quantenzustand in einen niedrigeren Energiezustand fallen.
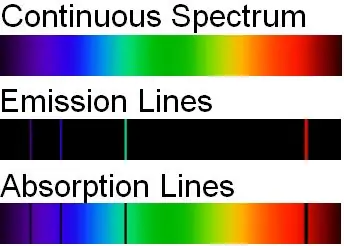
Abbildung 01: Vergleich von kontinuierlichen und diskreten Spektren (Emissions- und Absorptionslinien sind Beispiele für diskrete Spektren)
Im Allgemeinen haben quantenchemische Systeme diskrete Spektren, die normalerweise mit freien Teilchen assoziiert sind; somit sind Ort und Impuls eines freien Teilchens auf einen begrenzten Raum beschränkt, was zu einem diskreten Spektrum führt.
Was ist der Unterschied zwischen kontinuierlichem und diskretem Spektrum?
Ein kontinuierliches Spektrum ist eine Reihe von erreichbaren Werten einer physikalischen Größe, ohne beträchtliche Lücke zwischen den einzelnen Werten. Ein diskretes Spektrum ist eine Reihe erreichbarer Werte einer physikalischen Größe mit einer positiven Lücke zwischen jedem Wert. Der Hauptunterschied zwischen kontinuierlichem und diskretem Spektrum besteht darin, dass ein kontinuierliches Spektrum keine diskreten Linien aufweist, während ein diskretes Spektrum nur die diskreten Linien enthält. Daher ist ein kontinuierliches Spektrum eine kontinuierliche Reihe, während ein diskretes Spektrum separate Linien oder Werte hat. Darüber hinaus ist ein Spektrum eines leuchtenden Objekts ein Beispiel für ein kontinuierliches Spektrum, während das Absorptions- oder Emissionsspektrum isolierter Atome eines chemischen Elements ein Beispiel für ein diskretes Spektrum ist.
Die folgende Infografik zeigt die Unterschiede zwischen kontinuierlichem und diskretem Spektrum in tabellarischer Form.
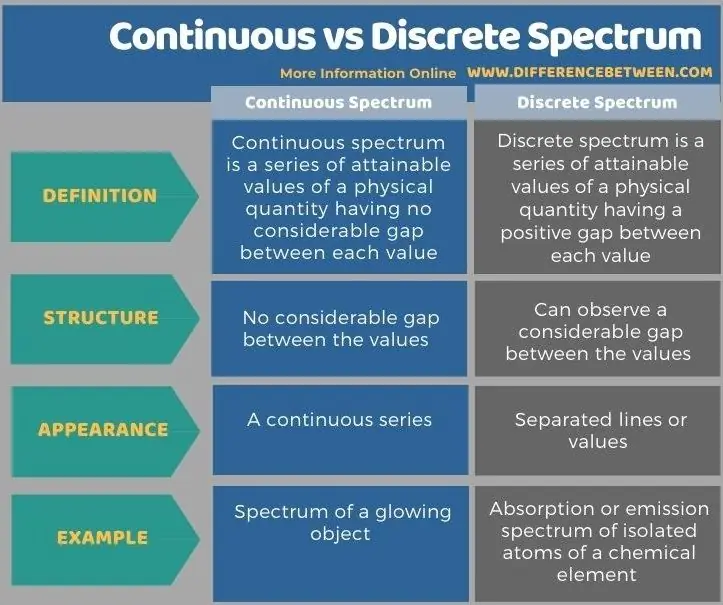
Zusammenfassung – Kontinuierliches vs. diskretes Spektrum
Kontinuierliches Spektrum und diskretes Spektrum werden normalerweise als das Gegenteil voneinander betrachtet. Der Hauptunterschied zwischen kontinuierlichem und diskretem Spektrum besteht darin, dass ein kontinuierliches Spektrum keine diskreten Linien aufweist, während ein diskretes Spektrum nur die diskreten Linien enthält.
